Schiefer Wurf
Schiefer Wurf berechnet aus Anfangsgeschwindigkeit, Winkel, Fallhöhe und Beschleunigung die Wurfweite, den höchsten Punkt, die Wurfzeit und Aufprallgeschwindigkeit bei einer konstanten Beschleunigung. Hier geht es zur neuen Online-Version mit erweiterten Features.| Programmdatei: | Schiefer Wurf.exe |
| Version: | 1.00 |
| Downloadgröße: | 37,5 KB |
| Größe auf der Festplatte: | 37,5 KB |
| Benötigte Dateien: | scint91.dll |
| Installation: | Lade das Programm herunter. |
| Bedienung: | Du startest das Programm und gibst die entsprechenden Werte ein. Nach einem Klick auf OK berechnet das Programm die anderen Werte. |
| Tipps: | Arbeite die Beispielszenarien durch. Die Werte für die Beschleunigung auf verschiedenen Planeten kannst du der beigefügten Hilfe entnehmen. |
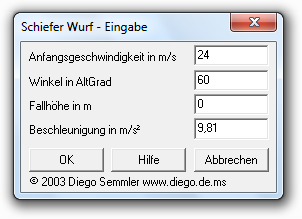
#1: Das Katapult
Die Römer werfen mit ihrem Katapult einen Stein. Als der Stein das Katapult verlässt, hat er eine Geschwindigkeit von 24 m/s und einen Winkel von 60°. Wie weit reicht das Katapult?Zunächst startest du das Programm und gibst folgende Werte ein: Anfangsgeschwindigkeit: "24" (denn es sind ja 24 m/s), Winkel in AltGrad "60". Die Fallhöhe kann auf null bleiben, denn das Katapult steht ja auf dem Boden. Auch die Erdbeschleunigung von 9,81 m/s² soll nicht geändert werden, da die Römer auf der Erde gelebt haben und die voreingestellte Beschleunigung somit richtig ist.
Ein Klick auf OK und das Programm rechnet. Hast du alles richtig gemacht, müssten die Römer ihren Stein ca 51 m weit und 22 m hoch geworfen haben.
#2: Fallendes Steinchen
Ein kleines Steinchen fällt vom Eiffelturm (161 m hoch). Mit welcher Wucht kommt es unten an?Du startest das Programm erneut. Diesmal kannst du Anfangsgeschwindigkeit und Winkel außer Acht lassen, denn das Steinchen wird nur fallen gelassen und nicht geworfen. Die Fallhöhe stellst du auf "161" und schon kann es los gehen.
Das Programm müsste nun ausgeben, dass das Steinchen 5,7 Sekunden unterwegs war und 56 m/s erreicht hat. Das sind ziemlich genau 200 km/h.
#3: Die Atombombe
Krieg auf dem Mars im Jahre 2220: Eine Atombombe wird aus einem Flugzeug aus 10 000 m Höhe abgeworfen. Das Flugzeug ist 720 km/h schnell und die Atombombe explodiert in 600 m Höhe. Wie weit vor dem Ziel muss die Bombe abgeworfen werden, damit sie trifft?Dies ist eine recht komplexe Aufgabe, da wir zunächst die Einheiten so umrechnen müssen, dass sie vom Programm verarbeitet werden. 720 km/h sind 200 m/s. Dies ist die Anfangsgeschwindigkeit. Der Winkel bleibt 0°, da das Flugzeug horizontal (also auch 0°) fliegt. Die Fallhöhe ist nicht 10 000 m, sondern 10 000 m -600 m also 9 400 m, da die Atombombe in 600 m Höhe explodieren soll. Auch die Beschleunigung muss diesmal geändert werden. Der Ortsfaktor für den Mars lautet nicht 9,81, sondern 3,72 (bitte eingeben). Jetzt ist wieder der Computer an der Reihe.
Der Computer sagt, die Bombe fliegt 14 218 m weit, braucht dafür 71 Sekunden und ist zur Explosion 332 m/s schnell (also fast Schallgeschwindigkeit). Die Bombe muss also nicht , wie man zunächst vermuten mag, direkt über dem Ziel abgeworfen werden, sondern 14,2 km vorher.
#4: Die Schleuder
Nach den letzten drei Beispielen dürfe es jetzt nicht schwer für dich sein folgende Aufgabe zu lösen:
Kinder auf einem 8 m hohem Baumhaus versuchen eine alte Dame, die auf einer 20 m entfernten Bank sitzt mit Schleudern abzuwerfen. Sie wissen, das man das beste Wurfergebnis, etwa mit 45° erzielt. Die Munition verlässt die Schleuder mit maximal 10 m/s.
Können sie die alte Dame treffen?